Вернуться к статье: Омаха с Жуком. Часть 3
Численное интегрирование по методу Симпсона.
Прежде чем мы начнем расчеты, давайте решим, каковы наши цели. Цель работы, проделанной в данном Приложении - найти ответ на следующий вопрос:
Чему ровна область ниже кривой распределения эквити на флопе между 0% и топ х% флопов?
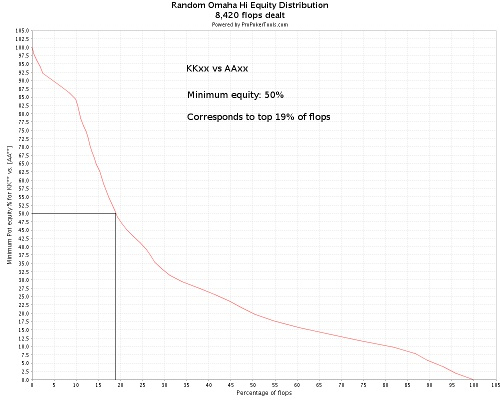
Например, мы с ККхх кладём оппонента на ААхх, нас интересует следующее: На скольких флопах ККхх будет иметь минимум 50% эквити против ААхх. На графике видно, что этот процент равен 19, как показано ниже: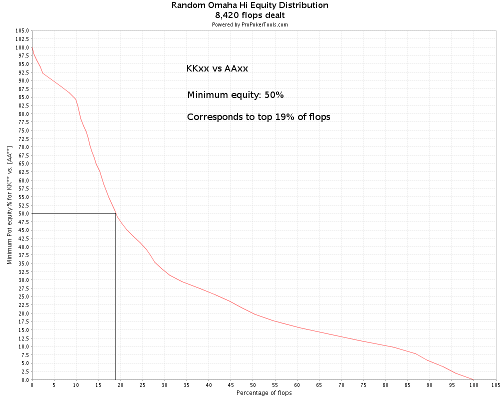
Затем был вопрос: Какова область ниже кривой распределения эквити на флопе между 0 и топ 19% флопов? Это выделенная область показана на рисунке ниже:
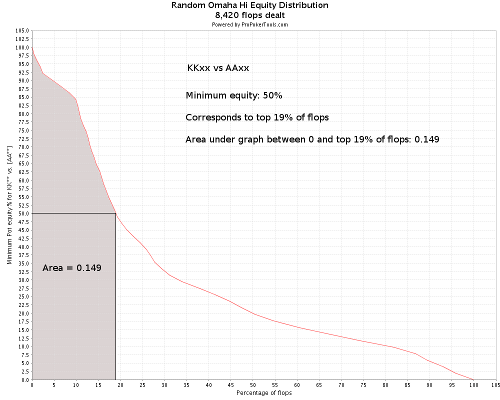
Теперь мы посчитаем эти значения, используя «Метод Симпсона» (Не Гомера!):
Вычисление значения области ниже кривой по методу Симпсона
Приблизительное значение области А {a, b} ниже кривой на интервале {a, b}(например, области ниже кривой распределения эквити на флопе между х=0 и х=1) может быть вычислено по формуле Симпсона:
A{a, b} =(1/6)(b-a){f(a) + 4f((a-b)/2) + f(b)}Где
f(a) = значение кривой в начальной точке - а
f(b) = значение кривой в конечной точке - b
(a-b)/2 = средняя точка между a и b
f((a-b)/2) = значение кривой в средней точке
Для того чтобы узнать, каким образом получились результаты, давайте посчитаем значение области ниже кривой в целом. Когда мы обсуждали распределение эквити на флопе, мы начали с того, что эквити ККхх против ААхх в целом равно всей области ниже кривой распределения эквити на флопе. С помощью ProPokerTools мы узнали, что это эквити равно 30,16%, соответственно, значение области ниже кривой распределения эквити на флопе равно 0,3016.
Теперь нам потребуется это значение для того, чтобы убедиться в точности метода Симпсона. Мы вычислим, чему равна область ниже кривой между 0 и 100% флопов и сравним наш результат с точным результатом.
Так как в данном случае отрезок кривой – эта вся кривая, мы работаем с большим интервалом {0, 1}. Поэтому для того, чтобы расчеты были более точными, мы разделим интервал на 10 субинтервалов {0, 0.10}, {0.10, 0.20}, ..., {0.90, 1.00} (чем меньше интервал, тем точнее будут расчеты по методу Симпсона). Мы вычислим значение области каждого субинтервала, и затем просто сложим результаты и получим общее значение.
Начнём с первого интервала {0, 0.10}. Сначала найдём значение (y) на кривой в начальной x =0, конечной x =0.10 и средней точке x =(0.10 - 0)/2 =0.05. Результаты будут иметь точность +/- 0.005
x =0.000 y =1.000
x =0.050 y =0.900
x =0.100 y =0.845
Мы вставим эти показатели в формулу Симпсона и получим следующее:
A{0, 0.10}=(1/6)(0.10 - 0.00){1.000 + 4(0.900) + 0.845}=0.0908
Поэтому область ниже кривой между x =0 и x =0.10 равна 0.0908. Затем мы рассчитаем области других субинтервалов A{0.10, 0.20}, A{0.20, 0.30}, ..., A{0.90, 1.00}. Ниже представлены все необходимые данные x и y для наших расчётов:
x =0.000 y =1.000
x =0.050 y =0.900
x =0.100 y =0.845
x =0.150 y =0.630
x =0.200 y =0.475
x =0.250 y =0.405
x =0.300 y =0.325
x =0.350 y =0.290
x =0.400 y =0.265
x =0.450 y =0.230
x =0.500 y =0.200
x =0.550 y =0.175
x =0.600 y =0.155
x =0.650 y =0.145
x =0.700 y =0.130
x =0.750 y =0.120
x =0.800 y =0.100
x =0.850 y =0.085
x =0.900 y =0.055
x =0.950 y =0.025
x =1.000 y =0.000
И вычисленные значения областей:
A{0.00, 0.10} =0.0908
A{0.10, 0.20} =0.0640
A{0.20, 0.30} =0.0403
A{0.30, 0.40} =0.0292
A{0.40, 0.50} =0.0231
A{0.50, 0.60} =0.0176
A{0.60, 0.70} =0.0144
A{0.70, 0.80} =0.0118
A{0.80, 0.90} =0.0083
A{0.90, 1.00} =0.0026
Область ниже кривой в целом равна:
A{0.00, 1.00}=0.0908 + 0.0640 + 0.0403 + 0.0292 + 0.0231 + 0.0176 + 0.0144 + 0.0118 + 0.0083 + 0.0026=0.3020
Что почти совпадает с точным результатом (0.3016). Таким образом, мы пришли к выводу, что формула Симпсона даёт нам более-менее точные данные об области ниже кривой.
Итак, наконец, мы вычислим значение области ниже кривой между 0% и топ 19% флопов, для этого разделим интервал {0.10, 0.19} на субинтервалы {0, 0.10}, {0.10, 0.19}
x =0.000 y =1.000
x =0.050 y =0.900
x =0.100 y =0.845
x =0.145 y =0.640
x =0.19 y =0.500
Формула Симпсона даёт нам следующие результаты:
A{0.00, 0.10} =0.0908
A{0.10, 0.19} =0.0586
Область ниже кривой между 0% и 19% флопов равна:
A{0, 0.19}=0.0908 + 0.0586=0.149
Это эквити ККхх против ААхх на топ 19% флопов в целом. Среднее эквити находится путём деления показателя эквити в целом на длину интервала (19%-0%=0,19-0=0,19):
Среднее эквити =0.149/0.19=0.784=78.4%
Теперь у нас есть все необходимые примеры для того, чтобы рассчитать среднее эквити на топ х% флопов для нашей руки/диапазона против руки/диапазона противника. Они помогут нам в наших будущих расчётах.
Пepевoд представлен при поддержке AdamevePoker.
Оригинал: Appendix to Part 3
