
Не все великие решения принимаются из-за кафедр, но ошибочно было бы предполагать, что наши решения были бы теми же, если бы не существовало лекторов и авторов книг, аккумулирующих, а затем передающих информацию своим аудиториям. Другое дело, что именно аудитории университетов становятся авангардом взаимодействия науки и общественности, приобретая тем самым образ «открытых дверей» в мир науки, однако, как быть с теми, кто не имеет доступа в аудитории?
Сейчас мы говорим не столько о пользе высшего образования, столько о количестве посредников между нами и непосредственно информацией. Важными в покере считаются концепции «теории вероятностей» и «теории игр». Я более, чем уверен, что вы слышали о них, но ведь не все открыли их, сидя в аудиториях. На просторах сети, читая книги, может даже просто обсуждая их с друзьями – вы получали доступ к информации, которая когда-то доносилась исключительно из уст представителей научного сообщества.
Мы попытаемся рассмотреть суть данных концепций, постараемся найти моменты для их приложения, а кроме того, сопроводим их примерами из игры. Для людей, владеющих английским, в конце каждого из параграфов, мы приложим ссылки на соответствующие онлайн-версии курсов, предложенные Гарвардским и Йельским университетами в рамках открытых образовательных программ.
Теория вероятностей

Основное содержание теории вероятностей заключается в разработке методов вычисления вероятностей одних случайных событий (относительно сложных) с помощью вероятностей других случайных событий (более простых), которые как-то связаны с первыми. Вероятности вторых, более простых, случайных событий в подавляющем большинстве реальных приложений теории вероятностей оценивают исходя из экспериментальных данных, проводя массовые однородные эксперименты. После этого с помощью формул теории вероятностей вычисляют вероятности более сложных событий (слово «случайных» в теории вероятностей обычно опускают), связанных с более простыми событиями, уже не проводя никаких экспериментов.
Однако, когда мы говорим о вероятности, то всегда имеем в виду вероятность наступления того или иного события. Понятие события является одним из основных понятий как общей аксиоматической теории вероятностей, так и наивной элементарной. Термин случайное событие используется в теории вероятностей только применительно к стохастическим экспериментам, а термин «событие» употребляется как сокращённая форма термина «случайное событие».
Мы не можем отдельно определить термины «случайное событие» (в смысле теории вероятностей) и «вероятность». Вероятностно-случайное событие – это случайное событие, которое имеет вероятность (что предполагает возможность неограниченного повторения эксперимента в неизменных условиях), а вероятность есть только у вероятностно-случайного события (у случайных событий, связанных с уникальными экспериментами, вероятности нет).
Важно понимать, что если речь идёт о событии, связанном с уникальным экспериментом, то сказать можно только одно: оно либо произойдёт, либо не произойдёт. Уникальные эксперименты со случайным результатом не являются предметом теории вероятностей.
В теории вероятностей важны: понятие «события», классическое «определение» вероятности; формула полной вероятности; формула Байеса; понятие независимых событий; понятие условной вероятности.

В приложениях теории вероятностей важно понимать следующее. Для реальных задач устойчивость частот наступления тех или иных событий, т.е. существование вероятностей этих событий, и значения вероятностей обычно устанавливаются в ходе экспериментов. Это даёт основание применять для расчёта вероятностей более сложных событий, связанных с изучаемым экспериментом, теоремы математической теории вероятностей. Однако, поскольку в реальности устойчивость частот и сами значения вероятностей исходных событий можно установить только приблизительно, нельзя гарантировать, что выводы, полученные с помощью этих теорем, применительно к изучаемому эксперименту верны хотя бы приблизительно (лучше сказать, с той степенью точности, с которой установлена устойчивость частот) – при удлинении цепочки логических умозаключений и увеличении числа операций, производимых с исходными вероятностями (которые в реальных задачах всегда известны только приблизительно), точность получаемых значений и достоверность окончательных выводов уменьшается.
Тем не менее, для покера данная концепция стала целым мировоззрением. Каждое принятое вами решение должно иметь математическое основание, строящееся на знании шансов и вероятностей. Популярными в сообществе являются готовые вероятностные таблицы, содержащие решения для всех типичных ситуаций. Насколько это может быть полезно? Если попытаться обобщить это в нескольких словах, то понятие «вероятности» в азартных играх существовало всегда, но понятие «математической вероятности» неразрывно связано с покером, как «игрой умения». На самом деле, примеры использования теории вероятностей очень широко представлены в жизни любого игрока. Некоторые из них, более других обладающие способностями «лектора», способны передать это знание, а главное, понимание – другим игрокам. Яркими примерами можно считать работы Раундера, Мошмана, Джанды и др. Помимо этих книг, как уже говорилось ранее, англоязычные пользователи могут ознакомиться с открытым курсом лекций Джо Блицштейна по ссылке.
Теория игр
Раздел математики, изучающий выбор оптимальных стратегий в конфликтных ситуациях, в рамках которого идет борьба между участниками, называется «Теория игр». Не стоит забывать, что каждая из сторон преследует свои интересы и ищет, прежде всего, наиболее выгодное решение, возможно (но необязательно), в ущерб соперникам. Теория игр позволяет выбирать с учетом информации об участниках взаимодействия, ресурсах, а также принимает во внимание возможные последствия принимаемых ими решений.
Теория игр обладает тенденцией к популяризации. Во многом, это связано с фамилиями Джона Харсаньи, Джона Нэша и Райнхарда Зельена, а также Роберта Аумана и Томаса Шеллинга.
Равновесие Нэша в покере - что это, очень простыми словами?
Для определения сути теории игр, следует обратиться к основным её определениям. Игра – математическая модель ситуации, характеризующаяся следующими характеристиками: наличие нескольких участников; неопределенность поведения участников; несовпадение их интересов; взаимосвязанность поведения участников (поскольку результат, получаемый каждым из них зависит от поведения всех участников); наконец, важным является наличие некоторых правил поведения, известных каждому из участников. Стратегия – совокупность правил, определяющих последовательность действий игрока в каждой конкретной ситуации, складывающейся в процессе игры. Партия – каждый из вариантов реализации игры. Ход – выбор игрока одного из допустимых решений. Исход игры – функция выигрыша, величина которой зависит от стратегии, примененной игроком.

Основой для процедуры расчёта в теории игр является выражение различных характеристик в количественной мере. В этом смысле мы обращаемся к «теории полезности» Дж. Фон Неймана и О. Моргенштерна, позиционирующей, что у решений существует функция полезности.
В зависимости от условий, существующих в момент принятия решения, теория игр квалифицирует процесс принятие решений на следующие квалификации: Во-первых, принятие решений в условиях определенности; Во-вторых, принятие решений в условиях риска; в-третьих, отдельно она рассматривает выборы в условиях неопределенности (что как раз относится к покеру); и, наконец, в-четвертых, теория игр особенно рассматривает принятие решений в условиях конфликтных ситуаций или противодействия противника.
Почему теорию игр следует помнить игрокам в покер? Теорема о минимаксе гарантирует, что каждая антагонистическая игра имеет оптимальные стратегии. Она даёт существование, но не определяет, как искать эти оптимальные стратегии. Помимо того, она обладает рядом специфических методов для каждого из видов игр и их особенностей, однако все они, так или иначе, упираются в методику определения полезности. А теперь снова вспомните книги Раундера, Мошмана, Джанды – ведь именно об этом они все говорят. Определение полезности решений в условиях неопределённости.

Давайте рассмотрим какую-нибудь из общеизвестных задач из теории игр в области покера. Задача настолько бородатая, насколько это вообще возможно. Интересно, кого-то еще удивит решение? Если нет, то благодарите тех, кто передал вам это знание, пусть оно и стало популярным и массовым - когда-то оно было прирогативой избранных.
2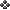 3
3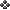 на доске A
на доске A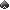 J
J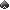 9
9 6
6 5
5
Банк составляет 1000$. Противник ставит 500$. Что мы выбираем? Фолд, Колл, или Рейз?
Теория игр, а если быть более точным, то теория полезности Дж. Фон Неймана говорит, что у каждого из наших решений есть функция полезности. В наших интересах извлекать максимальную выгоду. Давайте рассмотрим каждый из этих случаев.
Фолд: EV фолда равно 0. Всегда, это первое правило клуба (если вы понимаете о чем я).
Колл: EV колла в данной ситуации равно -500$. Я называю такую ситуацию блеф-коллом – порождением нашей гениальности. В нашем случае, единственный случай, когда мы не теряем дeньги – это дележка с другими 23.
Рейз: <1501$ поскольку после нашего рейза у соперника 2 варианта: он принимает нас, и мы теряем 1500$; фолдит, и мы забираем банк 1000$ + 500$ ставки соперника.
Обозначаем рейз как X, а фолд как Y, и да начнется математика (вернее, её глубокие микролимиты)
Соперник должен выбрать, так что X+Y=1
Тогда, X=1-Y
EV рейза 1500$ составит (1500)*(Y)+(-1500)*(1-Y) = 3000*(Y) – 1500
Мы выигрываем если,
3000Y-1500>0
3000Y>1500
Y = 1/2 (для нас считай Y>51%) - вероятность фолда, с которой соперник должен встречать ваш рейз, чтобы он был прибыльным.
Если вам хочется углубиться в эту тему, но понять саму концепцию теории игр, без насильной привязки к одним только играм в состоянии неопределенности, мы предлагаем англоязычным пользователям послушать курс открытых лекций профессора Йельского университета Бена Полака по ссылке.